A Neumann Problem for Inverse Mean Curvature Flow
In this talk we consider hypersurfaces with boundary which evolve in the direction of the unit normal with speed equal to the reciprocal of the mean curvature. We choose Neumann boundary conditions, i.e. the hypersurface moves along but stays perpendicular to a fixed supporting hypersurface. First we will concentrate on the case where the supporting hypersurface is a convex cone. In this case we obtain long time existence and convergence to a piece of a round sphere. Next we will present an approach to define weak solutions using a level set formalism which leads to a mixed Dirichlet-Neumann problem. This problem is then solved using the technique of elliptic regularization.

The evolution of hypersurfaces in asymptotically flat Riemannian manifolds by their inverse null mean curvature
We consider Riemannian manifolds which arise naturally as asymptotically flat initial data sets in general relativity. In this talk we introduce a new evolution equation for hypersurfaces in such manifolds where the> speed is given by the inverse null mean curvature. This PDE is motivated by the study of inverse mean curvature flow in asymptotically flat Riemannian manifolds and the study of marginally outer trapped surfaces in general relativity. Using level-set methods and elliptic regularisation, we define and prove existence of a unique weak solution for the flow under an appropriate curvature assumption on the initial data set.

Ricci flow on warped product R \times T^2 with hyperbolic ends, part I
What does Ricci flow do on M = R \times T^2 (T^2 is the 2 dimensional Torus) with warped product metric dx^2 + g^2(x)(dy^2+dz^2) (x \in R, (y,z) \in T^2, dy^2 + dz^2 is the standard flat metric induced by R^2, g: R \to R positive and smooth), such that the 2 ends of M are hyperbolic?
We show longtime existence, preservation of the warped product structure and that the (main) sectional curvatures (and so also |Rm|) go to 0 at least like 1/t....probably there is not enough time to do everything, so we might leave out some things or continue things in the next talk!

The Kato square root problem on vector bundles with generalised bounded geometry
We consider smooth, complete Riemannian manifolds which are exponentially locally doubling. Under a uniform Ricci curvature bound and a uniform lower bound on injectivity radius, we prove a Kato square root estimate for certain coercive operators over the bundle of finite rank tensors. We show that this coercivity condition is automatic for scalar-valued functions. These results are obtained as a special case of similar estimates on smooth vector bundles satisfying a criterion which we call generalised bounded geometry. We prove quadratic estimates for perturbations of Dirac type operators on such bundles and hence obtain a Kato square root type estimate under an appropriate set of assumptions.

 15:00 Uhr s.t.: Ricci flow on warped product R \times T^2 with hyperbolic ends, part IV

 16:00 Uhr c.t.: Stability of translating solutions to graphical mean curvature flow

 Ricci flow on warped product R \times T^2 with hyperbolic ends, part V

  15:00 Uhr s.t.: Ricci flow on warped product R \times T^2 with hyperbolic ends, part VI 

16:00 Uhr c.t.
Two-Phase Parabolic Obstacle Problem: Lµ-estimates for Derivatives of Solutions
Consider the two-phase parabolic obstacle problem with non-trivial Dirichlet condition

                      

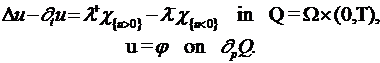
Here  is a given domain,  denotes the parabolic boundary of , and  are non-negative constants satisfying . The problem arises as limiting case in the model of temperature control through the interior.

In this talk we discuss the -estimates for the second-order space derivatives      near the parabolic boundary  . Observe that the case of general Dirichlet data cannot be reduced to zero ones due to non-linearity and discontinuity at  of the right-hand side of the first equation.

The talk is based on works in collaboration with Nina Uraltseva.

Dirac-harmonic maps, regularization and evolution equations
In the first part of the talk we will introduce the notion of Dirac-harmonic maps. They are critical points of an energy functional that is known as supersymmetric sigma model in theoretical physics. To this extend we will briefly discuss harmonic maps, harmonic spinors and focus under which assumptions they exist.
In the second part of the talk we will consider the evolution equations associated to Dirac-harmonic maps. To obtain a "nice" set of evolution equations we will perform a regularization of the energy functional for Dirac-harmonic maps. Finally we discuss long time existence, convergence and the dependence on the regularization of the evolution equations.